Math5620

Author: David Merkley

Language: Python

Description/Answers: This code solves a kinetics problem from the book using the forward Euler method. It calculates these solutions and plots them. Answers to the questions in the homework are going to be put in this section.

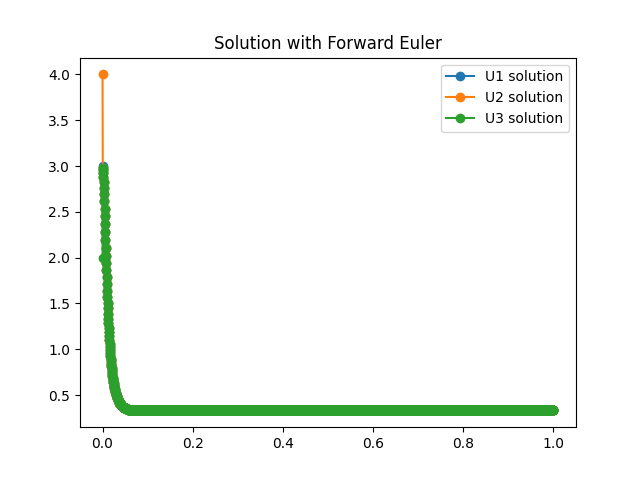
a). From Example 7.12 in the book, a matrix was used to find the eigenvalues of the system of equations from the kinetics problem. This led to the first eigenvalue being equal to -22. The other eigenvalues were equal to 0. This led to a bounding region where the k value had to be less than 1/17, so I chose the value to be 1/20 for this situation.

b). In practice, I started to see instability once the k value was equal to anything less than or equal to 1/12.

c). The same thing was done for when k1 was equal to 300 and k2 was equal to 1. An eigenvalue was found which led to the bounding region where the k value had to be less than 1/1650. This led to me choosing a value of k equal to 1/2000. In practice, I started to see instability once the value was anything less than or equal to 1/1600.

Implementation/Code:

from matplotlib import pyplot as plt
import numpy as np

# These are the different IVPs. Forward Euler is used to solve.
def U1(U1, U2, U3, k):
    return U1 + (k * ((-3 * U1 * U2) + U3))

def U2(U1, U2, U3, k):
    return U2 + (k * ((-3 * U1 * U2) + U3))

def U3(U1, U2, U3, k):
    return U3 + (k * ((3 * U1 * U2) - U3))

def main():
    # Lists that are used to hold the solutions.
    listU1 = [3]
    listU2 = [4]
    listU3 = [2]

    # This for loop puts all of the solutions into the lists.
    for n in range(1, 21):
        listU1.append(U1(listU1[n-1], listU2[n-1], listU3[n-1], n/20))
        listU2.append(U1(listU1[n-1], listU2[n-1], listU3[n-1], n/20))
        listU3.append(U1(listU1[n-1], listU2[n-1], listU3[n-1], n/20))

    # This information all plots the solution
    x2 = np.linspace(0, 1, 21)
    plt.plot(x2, listU1, marker='o', label='U1 solution')
    plt.plot(x2, listU2, marker='o', label='U2 solution')
    plt.plot(x2, listU3, marker='o', label='U3 solution')
    plt.title("Solution with Forward Euler")
    plt.xticks(x2)
    plt.legend()
    plt.show()

main()

Output:

K1 =3

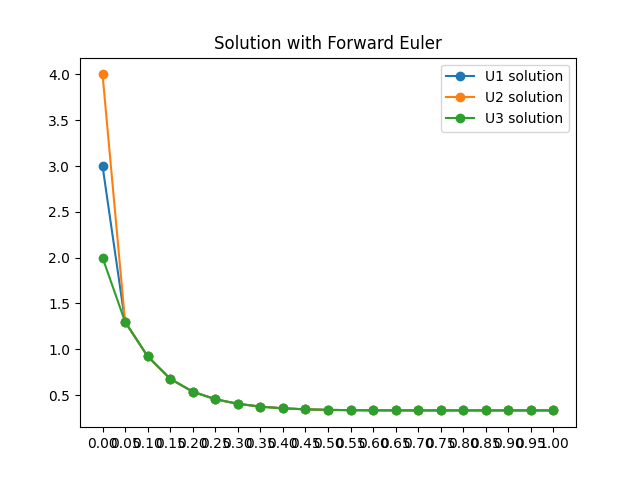
K1 = 300