Math5620

Author: David Merkley

Language: Python

Description/Purpose: This code solves a BVP, calculates the error, and calculates a 2-norm of the error. Then it plots all of this information.

Implementation/Code:

import numpy as np
from matplotlib import pyplot as plt
import math

# This is the function of u(x) when I take 2 derivatives of the original function. It is used to find U_hat.
def u(x):
    return -(math.sin(x)) + (2*x) + (math.sin(1)) - 1

# This is used to calculate the 2-norm for the error.
def L2Norm(x):
    return np.linalg.norm(x)

# This is where I coded the arrays and vectors and did all of the calculations to solve the equation and plot it.
def main():
    A = np.array([[-10, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0],
                 [100, -200, 100, 0, 0, 0, 0, 0, 0, 0, 0],
                 [0, 100, -200, 100, 0, 0, 0, 0, 0, 0, 0],
                 [0, 0, 100, -200, 100, 0, 0, 0, 0, 0, 0],
                 [0, 0, 0, 100, -200, 100, 0, 0, 0, 0, 0],
                 [0, 0, 0, 0, 100, -200, 100, 0, 0, 0, 0],
                 [0, 0, 0, 0, 0, 100, -200, 100, 0, 0, 0],
                 [0, 0, 0, 0, 0, 0, 100, -200, 100, 0, 0],
                 [0, 0, 0, 0, 0, 0, 0, 100, -200, 100, 0],
                 [0, 0, 0, 0, 0, 0, 0, 0, 100, -200, 100],
                 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]])
    F = np.array([1, math.sin(1/10), math.sin(2/10), math.sin(3/10), math.sin(4/10), math.sin(5/10), math.sin(6/10),
                  math.sin(7/10), math.sin(8/10), math.sin(9/10), 1])
    U = np.linalg.solve(A, F)
    U_hat = []
    for n in range(F.size):
        U_hat.append(u(n / 10))
    E = U - U_hat
    L2 = L2Norm(E)
    print("The solution U is:\n", U)
    print("The error of the solution is:\n", E)
    print("The 2-norm of the error is:\n", L2)
    x = np.linspace(0, 1, 11)
    y = np.linspace(-0.1, 1, 12)
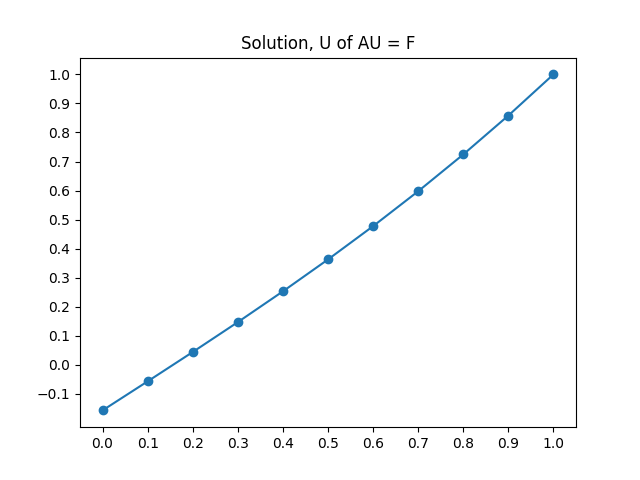
    plt.plot(x, U, marker='o')
    plt.title("Solution, U of AU = F")
    plt.xticks(x)
    plt.yticks(y)
    plt.show()
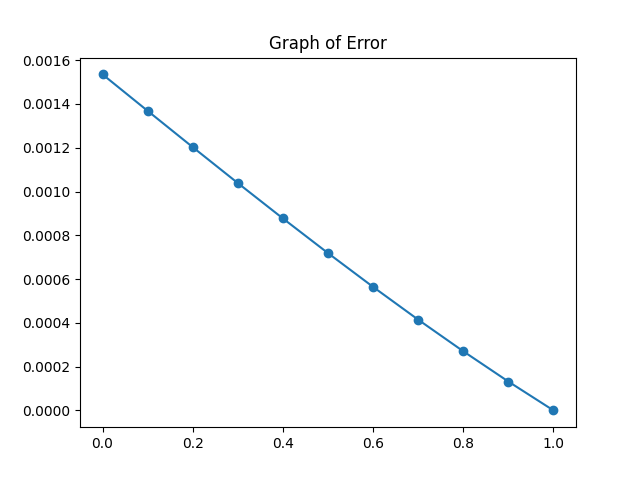
    plt.plot(x, E, marker='o')
    plt.title("Graph of Error")
    plt.show()

main()

Output:

The solution U is:
 [-0.15699397 -0.05699397  0.04400437  0.1469894   0.25292962  0.36276404
  0.47739271  0.5976678   0.72438507  0.8582759   1.        ]
The error of the solution is:
 [0.00153505 0.00136847 0.00120271 0.00103862 0.00087698 0.00071859
 0.00056419 0.0004145  0.00027018 0.00013182 0.        ]
The 2-norm of the error is:
 0.0029360330838805212